0x00 引言
本文主要知识结构与素材摘自《基于深度学习的计算机视觉》[1]。
计算机视觉是一门研究如何使机器“看”的科学,更进一步的说,就是是指用摄影机和电脑代替人眼对目标进行识别、跟踪和测量等机器视觉,并进一步做图形处理,使电脑处理成为更适合人眼观察或传送给仪器检测的图像。
计算机视觉与机器视觉是很相近的词汇,计算机视觉主要是指使计算机获得视觉能力,而机器视觉所指更广泛一些,包括工业上使用的机器获得视觉能力,又比如机器人的视觉能力等。
计算机视觉目前主要有两个研究维度,包括几何属性和语义感知。几何属性比较直观一些,而语义感知更加智能化,比如识别物体以及物体之间的位置关系等。其当前主要研究领域如下图所示:
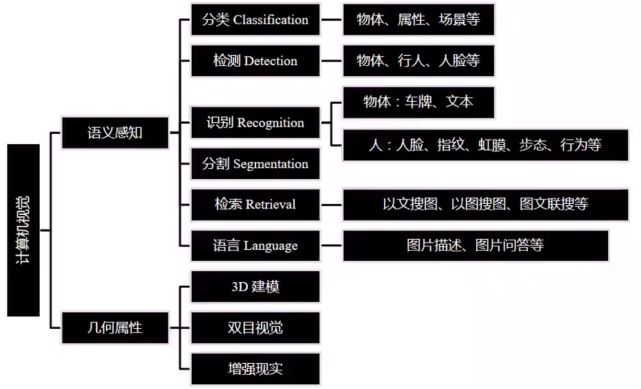
0x01 图像数据处理
要使计算机获得视觉能力,则首要的一步就是对图像进行处理,以获取最佳的素材图片。本节的研究内容概况如下图所示:
1 | 1 图片存储原理 |
1、图片存储原理
一张图的数字化显示方式有许多,目前常用的方法有:
1)RGB颜色空间。即用三原色组合。
2)CMY(K)颜色空间。用于打印机彩打。
3)HSV/HSL(I)颜色空间。人类的视觉概念。H,色调;S,饱和度;V,明度;L,亮度。
4)CIE-XYZ颜色空间。基于人类颜色视觉的直接测定。
5)CIE-Lab颜色空间。接近人类视觉、致力于感知均匀性
最主流的颜色空间即RGB颜色空间,在硬件上,会用到基于Bayer网格的颜色传感器。
2、空域分析及变换(卷积/滤波)
卷积/滤波是在图像处理之前很重要的一个步骤,其核心思想就是对像素点附近的点根据权重做数学运算,如下图所示:
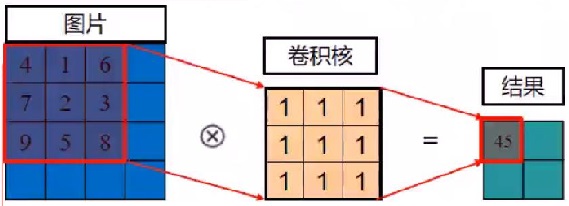
很多人认为卷积就是滤波,两者并无区别,其实不然。两者在原理上相似,但是在实现的细节上存在一些区别[2]。
卷积/滤波过程是对图片中所有像素点做变换,那么边界像素点的周围像素是不全的,那么就需要对图片做边界补充[3],具体的补充方法有补零、边界复制、镜像以及块复制。
卷积/滤波的最终目的是对图像进行处理,所以根据卷积核数学操作的不同,可以对图片进行不同的操作[3],例如:
1)平滑均值滤波/卷积(均值滤波)。该操作是为了抑制噪声,使图像亮度趋于平缓的处理方法就是图像平滑。图像平滑实际上是低通滤波,平滑过程会导致图像边缘模糊化。
2)平滑中值滤波(中值滤波)。作用与均值滤波一样,比如用于去除椒盐噪声。
3)平滑高斯滤波/卷积(高斯滤波)。高斯平滑水平和垂直方向呈现高斯分布,更突出了中心点在像素平滑后的权重,相比于均值滤波而言,有着更好的平滑效果。
4)梯度Prewitt滤波/卷积。对水平边缘或垂直边缘有比较好的检测效果。
5)梯度Laplacian滤波/卷积。Laplacian也是一种锐化方法,同时也可以做边缘检测,而且边缘检测的应用中并不局限于水平方向或垂直方向
3、频域分析及变换
3.1、傅里叶变换
傅里叶变换[4]想要表达的就是一个信号可以由足够多个不同频率和幅值的正余弦波组成。
有了理论基础,接下来就是对图片进行二维傅里叶变换[5]。(理论不是很懂,现在有了神经网络之后,这种变换就很少用了,所以…)
4 图像金字塔
图像金字塔是一种以多分辨率来解释图像的结构,通过对原始图像进行多尺度像素采样的方式,生成N个不同分辨率的图像。把具有最高级别分辨率的图像放在底部,以金字塔形状排列,往上是一系列像素(尺寸)逐渐降低的图像,一直到金字塔的顶部只包含一个像素点的图像,这就构成了传统意义上的图像金字塔[6]。
一般情况下有两种类型的图像金字塔常常出现在文献和以及实际运用中。他们分别是高斯金字塔与拉普拉斯金字塔。两者的简要区别[7]:高斯金字塔采用下采样,而拉普拉斯金字塔则用来上采样重建一个图像。
4.1 高斯金字塔
高斯金字塔能够用来捕捉不同尺寸的物体。之所以要采用高斯滤波加图像金字塔模式的原因是:其一在多次高斯卷积之后,一些像素是多余的,所以要做图像金字塔;其二如果不采用高斯滤波就直接降采样的话,会损失图片原有信息。具体操作过程看博文[7]。
4.2 拉普拉斯金字塔
高斯金字塔会导致高频信息在下采样过程中丢失。而拉普拉斯金字塔采用上采样,能够保留所有层所丢失的高频信息,用于图像恢复
5 模板匹配
模板匹配是一种最原始、最基本的模式识别方法,研究某一特定对象物的图案位于图像的什么地方,进而识别对象物,这就是一个匹配问题。其作用是同尺度目标的检测(阴阳师辅助外挂里就用了这个,哈哈!)。
模板匹配有六个方法[8],可以了解一下。
6 特征数据操作
6.3 聚类/Cluster
目标是找出混合样本中内在的组群关系。其常用的方法有:
1)Kmeans[9]
2)EM算法
3)Mean shift
4)谱聚类
5)层次聚类
0x02 图像特征及描述
经过图像处理后的图片素材,接下来需要通过图像特征及描述来获取图片中的重要信息。本节内容是在神经网络流行之前计算机视觉常用的一些知识。本节的研究内容概况如下图所示:
1 | 1 颜色特征 |
1 颜色特征
1.1 直方图
没什么好讲的,就是数据统计用的直方图。
1.2 量化颜色直方图
适用于均匀的颜色空间,比如RGB、HSV等,其属性坐标系如下图所示:
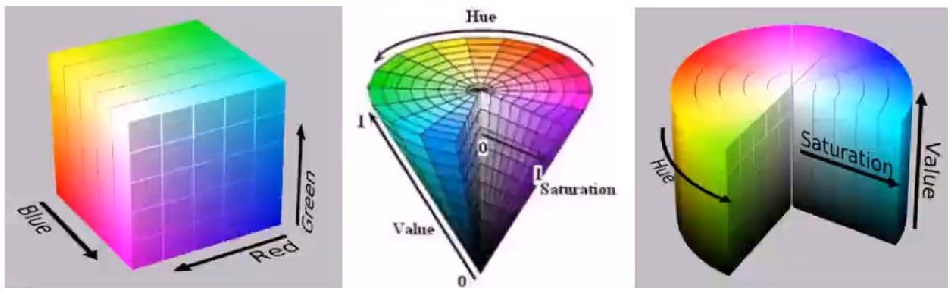
1.3 聚类颜色直方图
适用于非均匀的颜色空间,例如Lab。操作过程需要先使用聚类算法(例如Kmeans)对所有像素点颜色向量进行聚类。
2 几何特征
2.1 边缘/Edge
像素明显变化的区域,一般具有丰富的语义信息,该特征主要用于物体识别、几何与视角变换等。
边缘提取操作过程为先高斯去噪,再使用一阶导数获取极值。先使用高斯去噪的原因是导数对噪声敏感。
二维高斯函数如下所示:
$$h_{\sigma }\left ( u,v \right )=\frac{1}{2\pi \sigma ^{2}}e^{-\frac{u^{2}+v^{2}}{2\sigma ^{2}}}$$
其在x方向上的一阶导数可表示为:
$$h_{x}\left ( x,y \right )=\frac{\partial h\left ( x,y \right )}{\partial x}=\frac{-x}{2\pi \sigma ^{4}}e^{-\frac{x^{2}+y^{2}}{2\sigma ^{2}}}$$
其在y方向上的一阶导数可表示为:
$$h_{y}\left ( x,y \right )=\frac{\partial h\left ( x,y \right )}{\partial y}=\frac{-y}{2\pi \sigma ^{4}}e^{-\frac{x^{2}+y^{2}}{2\sigma ^{2}}}$$
上式中的变量$\sigma $即为标准差,该值越大,高斯函数的峰值越小,范围越宽,该变量对于边缘提取的尺度有影响。
根据周围像素之间变化程度可以做出梯度向量,梯度(增加最快)的方向可以表示为:
$$arctan\left ( \frac{h_{y}\left ( x,y \right )}{h_{x}\left ( x,y \right )} \right )$$
梯度幅值/强度可以表示为:
$$h_{x}\left ( x,y \right )^{2}+h_{y}\left ( x,y \right )^{2}$$
矢量的箭头方向表示梯度增加最快的方向,矢量的大小用箭头的长度表示,矢量可如下图表示:

不同标准差的滤波捕捉到不同尺度的边缘。其变化可从下图看出:

2.2 兴趣点/关键点
兴趣点/关键点是指稳定的局部特征点,其特点是可重复性与显著性,这类点能够抗图片变换,例如当图片的外貌变换(亮度、光照)以及几何变换(平移、选择、尺度)发生时,仍然能够捕捉到该点。
兴趣点/关键点主要运用在图片配准/拼接、运动跟踪、物体识别、机器人导航以及3D重建。(ROS里的find_object功能包应该就用到了特征点检测)
2.3 Harris角点/Corner
如果在任何方向上移动小观察窗,导致大的像素变动的点,肯定是一个角点,其原理如下图所示:
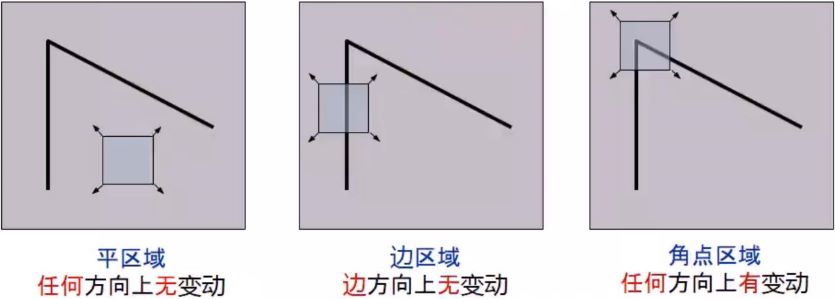
2.4 斑点/Blob
斑点即一阶极值点或者说是二阶导数零点,这种点对噪声很敏感,需要先做高斯平滑。斑点检测通常也被称为兴趣点检测或者兴趣区域检测,即兴趣点经常指斑点。
3 局部特征
*3.1 SIFT关键点
SIFT的全称是Scale Invariant Feature Transform,尺度不变特征变换,由加拿大教授David G.Lowe提出的。SIFT特征对旋转、尺度缩放、亮度变化等保持不变性,是一种非常稳定的局部特征。
SIFT算法的原理可见博文[10]。
3.1 SURF关键点
SURF算法采用均值滤波与积分图像,其计算速度比SIFT快6倍,但是精度不如SIFT。
4 纹理特征
4.1 方向梯度直方图/HOG
是一种对图像局部重叠区域的密集型描述符, 它通过计算局部区域的梯度方向直方图来构成特征。
是具体计算过程看博文[11]。如果需要检测物体,还需要配合如SVM分类器。
4.2 局部二值模式/LBP
LBP(Local Binary Pattern,局部二值模式)是一种用来描述图像局部纹理特征的算子;它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikäinen, 和D. Harwood 在1994年提出,用于纹理特征提取。而且,提取的特征是图像的局部的纹理特征。
具体计算过程看博文[12]。如果需要检测物体,还需要配合如SVM分类器。
4.3 滤波器组/Gabor
0x03 引用文献
[1]http://www.chinahadoop.cn/course/916
[2]https://blog.csdn.net/haoji007/article/details/53911940
[3]https://www.cnblogs.com/xiaojianliu/p/9075872.html
[4]https://www.cnblogs.com/h2zZhou/p/8405717.html
[5]https://blog.csdn.net/thecentry/article/details/80709593
[6]https://www.cnblogs.com/jiahenhe2/p/7919356.html
[7]https://blog.csdn.net/xbcreal/article/details/52629465
[8]https://www.cnblogs.com/skyfsm/p/6884253.html
[9]https://www.cnblogs.com/bourneli/p/3645049.html
[10]https://blog.csdn.net/weixin_38404120/article/details/73740612
[11]https://www.cnblogs.com/zhazhiqiang/p/3595266.html
[12]https://blog.csdn.net/heli200482128/article/details/79204008
