0x00 引言
Powell在1985年提出了多变量插值的径向基函数(RBF)方法;1988年,Broomhead和Lowe首先将RBF应用于自适应神经网络的设计中,从而构成了RBF神经网络;1990年,Poggi和Girosi发表两篇论文,将正则化理论应用于RBF神经网络。其特点是结构简单、训练简洁、学习收敛速度快、能够以任意精度逼近任意连续函数[1]。
0x01 RBF神经网络基本结构
与BP神经网络类似,径向基神经网络是一种含三层神经元的前馈神经网络,分别是输入层、隐含层以及输出层,其基本结构如下图所示[2] :
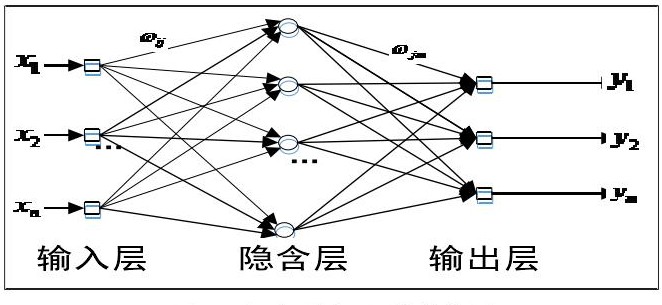
RBF网络的基本思想是:用RBF作为隐单元的“基”构成隐含层空间,这样就可以将输入矢量直接映射到隐空间,而不需要通过权连接。当RBF的中心点确定以后,这种映射关系也就确定了。而隐含层空间到输出空间的映射是线性的,即网络的输出是隐单元输出的线性加权和,此处的权即为网络可调参数。其中,隐含层的作用是把向量从低维度的p映射到高维度的h,这样低维度线性不可分的情况到高维度就可以变得线性可分了,主要就是核函数的思想。这样,网络由输入到输出的映射是非线性的,而网络输出对可调参数而言却又是线性的。网络的权就可由线性方程组直接解出,从而大大加快学习速度并避免局部极小问题。
第一层:输入层。与BP神经网络输入层含义相同,为输入向量X。
第二层:隐含层。网络中仅有的隐含层,作用是实现输入空间到隐含空间的非线性变换,这种变换是通过隐含节点的径向基函数实现的。该层即RBF与BP神经网络区别所在,与BP神经网络的激活函数(sigmoid函数)不同,RBF神经网络的激活函数一般取以下三种[1]:
1)高斯函数:
$$\varphi \left ( x \right )=exp\left ( -\frac{x^{T}x}{\sigma ^{2}} \right )$$
2)逆多二次函数:
$$\varphi \left ( x \right )=\frac{1}{\left ( x^{T}x+\sigma ^{2} \right )^{\frac{1}{2}}}$$
3)反射sigmoid函数:
$$\varphi \left ( x \right )=\left ( 1+exp\left ( \frac{x^{T}x}{\sigma ^{2}} \right ) \right )^{-1}$$
其中最常用的径向基函数是高斯核函数:
$$\varphi \left ( x,u_{i} \right )=exp\left ( -\frac{\left | x-u_{i} \right |^{2}}{2\sigma_{i} ^{2}} \right ), , , i=1,2,\cdots ,n$$
式中,$u_{i}$表示神经元i的核函数中心向量;$\sigma _ {i}$表示核函数的宽度参数,控制核函数的径向作用范围。
第三层:输出层。隐含层到输出层为线性映射:
$$y=\sum_{i=1}^{n}w_{i} \varphi \left ( x,u_{i} \right )+b$$
式中,$w_{i} $为权重,b为偏置。
0x01 RBF神经网络学习算法[3]
在上一节中提到的高斯核函数为隐含层的网络结构如下图所示:
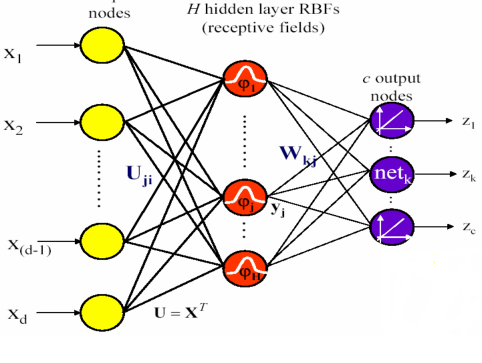
学习算法的整个流程可以大致如下图:
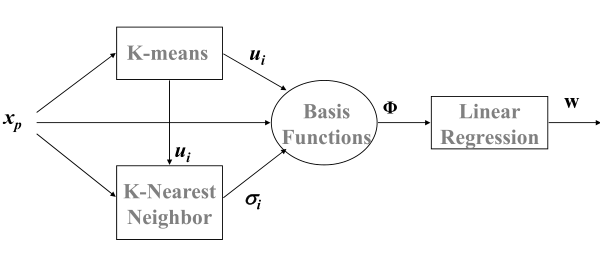
其算法过程具体描述为:
1)利用K-means算法寻找核函数中心向量$u_{i}$
2)利用KNN计算核函数宽度参数$\sigma _ {i}$
3)利用最小二乘法求得权重$w_{i} $
(可以看到该过程让人一头雾水..)后来有人提出了lazy RBF,又称为固定法,即定义隐含单元的径向基函数的中心向量是固定值,具体过程可用下图表示:

0x03 引用文献
[1]神经网络控制与MATLAB仿真
[2]https://www.cnblogs.com/pinking/p/9349695.html
[3]https://blog.csdn.net/weiwei9363/article/details/72808496
