C++数据结构

2018-10-21 阅读量

0x00 引言

数据结构是以某种特定的布局方式存储数据的容器。
在C++标准库中，STL(标准模板库)就借助类模板把常用的数据结构及其算法都实现了一遍，并且做到了数据结构和算法的分离。另外也可以使用boost库。
常用的数据结构为以下八种:

0x01 容器-向量元素连接结构
  1 数组
  2 链表
  3 树
  4 图
  5 哈希表
0x02 容器适配器-向量元素特殊增删方式
  1 栈
  2 队列

0x01 容器-向量元素连接结构

向量是由一组数据组合成的，但在计算机存储元器件内，需要以特定的方式连接。连接方式可分为静态连接(数组)与动态连接(链表)。

1 数组
  1.1 静态数组-array
  1.2 动态数组
    1.2.1 vector
    1.2.2 priority_queue
    1.2.3 deque
    1.2.4 stack
    1.2.5 queue
2 链表
  2.1 单向链表-forward_list
  2.2 双向链表-list
3 树    
  3.1 搜索树
    3.1.1 二叉树
    3.1.2 平衡二叉树
    3.1.3 AVL树
  3.2 高级搜索树
    3.2.1 红黑树
      3.2.1.1 map
      3.2.1.2 set
      3.2.1.3 multimap
      3.2.1.4 multiset
4 图
  4.1 图论
    4.1.1 基本概念
    4.1.2 图的矩阵表示
5 哈希表
  5.1 基本概念
  5.2 散列法

1、数组
以数组方式存储的向量，在内存空间的存储形式是连续的，因此又称为静态连接。在C++中，其对应的类为std::vector。
相比于动态连接的链表，数组方式数据存储效率更高;缺点是当要在元素中间插入新元素时效率很低，因插入过程为将插入位置后续元素均后移再插入新元素。所以std::vector插入新元素时多为栈(下一章节)的方式，即push_back/emplace_back。

2、链表
链表就像一个节点链，其中每个节点包含着数据和指向后续节点的指针，因此又称为动态连接。在C++中，其对应的类为std::list。
相比于静态连接的数组，链表在任意位置插入新元素的效率更高，因为新增元素时只需要修改上一元素指针指向及该元素指针指向;缺点是数据存储效率较低。所以当向量元素增删方式为队列(下一章节)时，元素之间的连接结构常用链表。

3、树
假设现在需要维护关于一亿人口信息的数据库。如果用数组实现，虽然存储效率高，但是每修改一个用户信息，需要判断最多一亿次，且没插入数据将非常慢；如果用链表实现，虽然能够实现插入数据，但是每修改一个用户信息，仍然需要判断最多一亿次。
树是一种层次化结构，从文件系统、互联网域名系统和数据库
系统，一直到地球生态系统乃至人类社会系统，层次化特征以及层次结构均无所不在。
树的结构及各个部分名词如下，其中度表示该节点有多少个子节点:

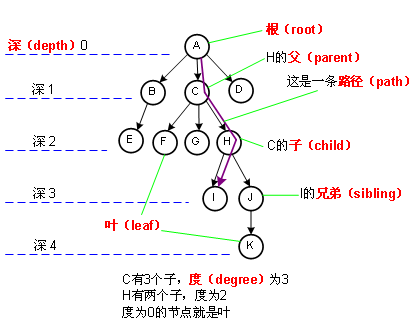
3.1、搜索树
3.1.1、二叉树
所谓二叉树的概念是指，所有的节点其子节点小于等于2的树。
**3.1.2、平衡二叉树**
现在想想我们的目标，是希望尽可能用更少的搜索次数在树内搜索到目标，那么等价于树的深度尽可能小。假如有数组[1,2,3]，则可生成如下图所示五种树，最后一种的搜索速度最快:

3.1.3、AVL树
所谓AVL树，是指所有节点的左右子树高度差不大于1的树。
AVL优点是查询速度非常快(平衡性好);缺点是每个节点都需要存储一个int型数据(-1,0,1)，用于表达左右子树的高度差，且旋转频次更高。AVL多用于数据库。

3.2、高级搜索树
通过对任何一条从根到叶子的简单路径上各个节点的颜色进行约束，确保没有一条路径会比其他路径长2倍，因而是近似平衡的。所以相对于严格要求平衡的AVL树来说，它的旋转保持平衡次数较少。用于搜索时，插入删除次数多的情况下我们就用红黑树来取代AVL。
实际应用中，C++ STL(map、set)均基于红黑树。其原理可能较为难理解，具体介绍看视频^[1]。红黑树举例如下图:

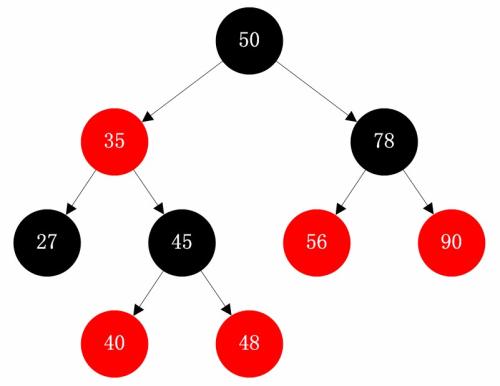
红黑树必须满足如下性质:1)根节点必须为黑色;2)父子节点不能同为红色;3)从根节点出发到任意叶子节点，黑色节点数量必须一致。

4、图
树是一种层次化结构，可以方便地用来描述种属关系。但是现实世界中，很多问题并不是这种从根往下衍生的关系，比如社交网络或者运输网络等，这时图的作用即可体现。
**4.1、图论**
图论是数学的一个分支，它以图为研究对象。图论中的图是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。
以下内容摘自视频^[2]。

4.1.1、基本概念
1) 有向图与无向图
无方向的图为无向图，有方向的图为有向图，其中圆圈称为”结点”，连接线称为”边”:

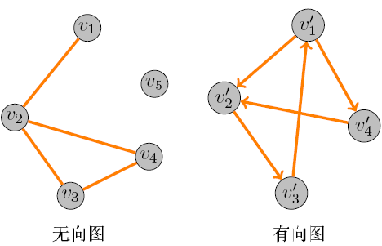
2) 简单图与多重图
如下图所示，结点v1有一两端重合的边e1，即为”环”;结点v2、v3之间有两条边，即为”多重边”。既没有环也没有重边的图称为”简单图”;含多重边的图称为”多重图”。

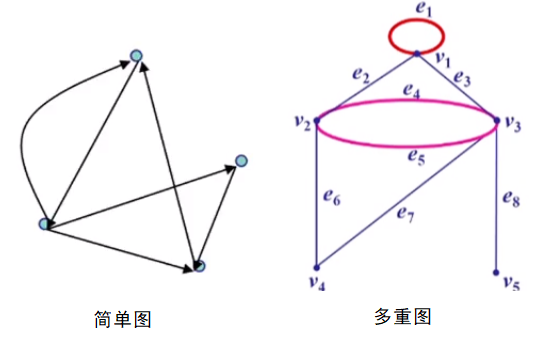
3) 完全图与赋权图
任意两顶点都相邻的简单图称为”完全图”，如果给其边上加权重，则称为”多重图”。

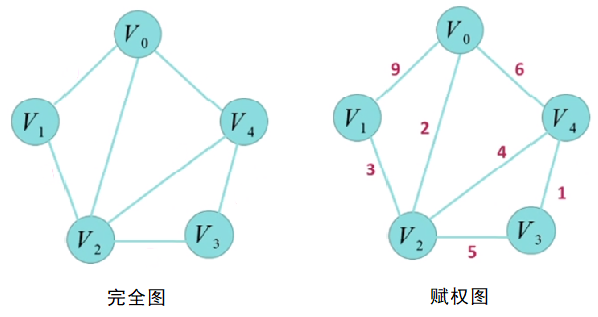
4.1.2、图的矩阵表示
1) 邻接矩阵
$$A=\left ( a_{ij}\right )_{n\times n}$$

$$a_{ij}=\begin{cases}
1 & v_iv_j \in E \\
0 & v_iv_j \notin E
\end{cases}$$

2) 权矩阵
$$A=\left ( a_{ij}\right )_{n\times n}$$

$$a_{ij}=\begin{cases}
F(v_iv_j) & v_iv_j \in E \\
0 & i=j \\
\infty & v_iv_j \in E
\end{cases}$$

5、哈希表
除了树和图，还有一种寻址容易，插入删除也容易的数据结构哈希表^[3]，哈希表也叫散列表，是根据关键码值(key)而直接进行访问的数据结构。
**5.1、基本概念**
哈希表实质上就是一个元素为链表的数组，而原来数组下标更改为了key，其计算方法是通过某种算法将hash值转换得到，这种算法叫做”散列法”，其对应的映射函数叫做”散列函数”，存放记录的数组叫做”散列表”。

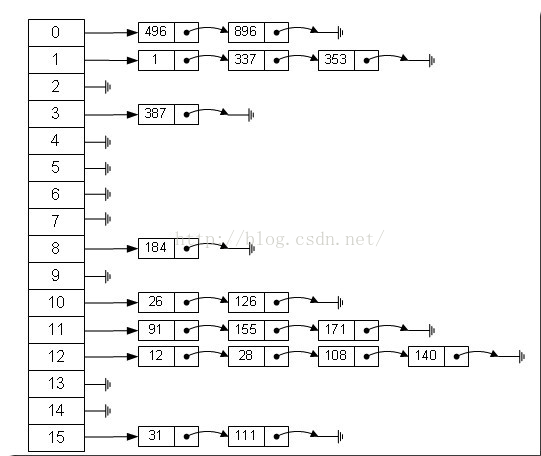
5.2、散列法
散列法有:除法散列法、平方散列法、斐波那契(Fibonacci)散列法。

0x02 容器适配器-向量元素特殊增删方式

在数组或链表中，向量元素的增删除了任意选定需要增删的元素之外，还有两种常用的特殊增删方式。即栈和队列，前者可描述为元素”后进先出”，而后者可描述为元素”先进先出”。

1
2

1 栈
2 队列

1、栈
以栈的方式增加向量元素时，是从向量末尾开始新增;以栈的方式删减向量元素时，是删除向量末尾的元素。因此栈的元素增删可形象地描述为”后进先出”，可参考如下图:

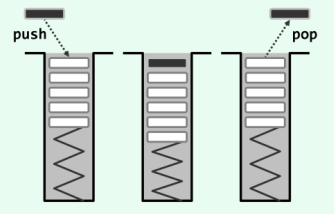
C++ STL中提供了容器适配器，来直接指定具有栈功能的容器，其类名为std::stack。stack容器适配器的模板有两个参数，第一个参数是存储对象的类型，第二个参数是底层容器的类型，默认为deque。

2、队列
以队列的方式增加向量元素时，是从向量末尾开始新增;以栈的方式删减向量元素时，是删除向量首部的元素。因此栈的元素增删可形象地描述为”先进先出”，可参考如下图:

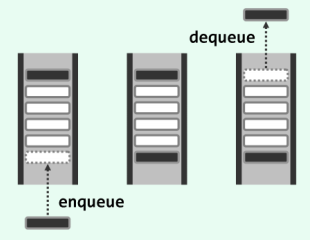
C++ STL中提供了容器适配器，来直接指定具有队列功能的容器，其类名为std::queue。queue容器适配器的模板有两个参数，第一个参数是存储对象的类型，第二个参数是底层容器的类型，默认为deque。

0x03 引用文献

[1]https://www.bilibili.com/video/av45909616?from=search&seid=17043173083215253621
[2]https://www.bilibili.com/video/av88139911?from=search&seid=15931070673176572409
[3]https://blog.csdn.net/yyyljw/article/details/80903391